starnfc.blogg.se - Flux integral cylindrical coordinates paraboloid

#FLUX INTEGRAL CYLINDRICAL COORDINATES PARABOLOID HOW TO#
#FLUX INTEGRAL CYLINDRICAL COORDINATES PARABOLOID FREE#

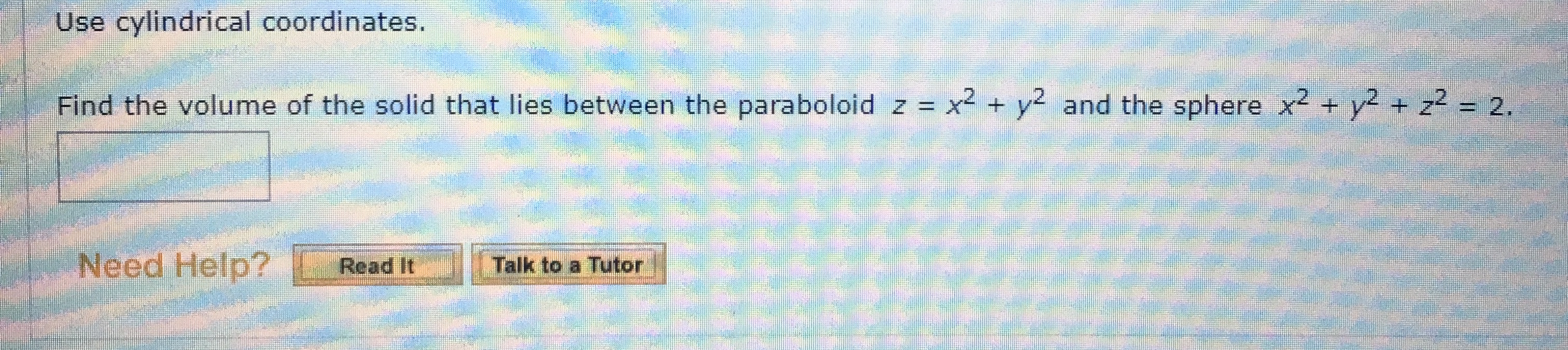
There are two parts to the boundary of R, the paraboloid and a unit disk in the plane z = 1. Obtain the volume integral of the divergence of FĬontext Panel: Student Multivariate Calculus≻Integrate≻IteratedĬomplete the dialogs as per the figures below.ĭivF = y 3 + x 2 + z → MultiInt ∫ − 1 1 ∫ − − x 2 + 1 − x 2 + 1 ∫ x 2 + y 2 1 y 3 + x 2 + z &DifferentialD z &DifferentialD y &DifferentialD x = 5 12 ⁢ &pi integrals (it is a mathematical generalization of Gauss Flux Theorem.

#FLUX INTEGRAL CYLINDRICAL COORDINATES PARABOLOID HOW TO#

F = y 3 + x 2 + z → assign to a name divF how to set up multiple integrals in cylindrical and spherical coordinates as.

F, the divergence of F, and represent it parametricallyĬommon Symbols palette: Del and dot-product operators.

X y 3, y z, x 2 z = → to Vector Field → assign to a name F we use the vector for the normal direction.

Taking the limit of that sum as the diagonal of the largest rectangle goes to 0 gives.

#FLUX INTEGRAL CYLINDRICAL COORDINATES PARABOLOID FREE#

Press the Access Settings button and selectĮnter the components of F in a free vector.Ĭontext Panel: Evaluate and Display InlineĬontext Panel: Student Vector Calculus≻Conversions≻To Vector Field Thus, the total surface area S of is approximately the sum of all the quantities r u × r v u v, summed over the rectangles in R. In3(b), we found r u r v h ucosv usinv ui. Tools≻Load Package: Student Vector Calculus ux integral is ZZ S 1 FdS ZZ R F(r(u v)) (r u r v) dA: To nd F(r(u v)), we just plug our parameterization into F(x y z) h0 0 zi, which gives F(r(u v)) h0 0 ui. ) can be measured with the following line integral: d ( fluid mass in region) d t Rate at which mass leaves region C F n d s. , the rate at which fluid is exiting that region (assuming it has density. The triple integral can be calculated by using the spherical coordinates. start color 0c7f99, F, end color 0c7f99, left parenthesis, x, comma, y, right parenthesis. Hence, the Student MultivariateCalculus package is installed to gain Context Panel access to the MultiInt command. (a) F(x, y, z) xy i+yz j+zxk, S is the part of the paraboloid z 4x2 y2. The Student VectorCalculus package is needed for calculating the divergence, but it then conflicts with any multidimensional integral set from the Calculus palette.

The total flux is then 1 6 + 1 4 &pi = 5 12 &pi, the same value obtained for the volume integral of the divergence, as predicted by the Divergence theorem. ∫ 0 2 &pi ∫ 0 1 r ⋅ r cos &theta 2 dr d &theta = &pi 4 The sphere x2 + y2 + z2 9 has representation. Implementing the flux integral in polar coordinates gives The paraboloid z x2 + y2 has representation using cylindrical coordinates as x r cos, y r sin, z r2.

N = x 2 z, which becomes x 2 in the plane z = 1.

On the upper boundary (disk), the outward normal is N = k, so F If this be integrated over the unit disk, the result is

2 x 2 y − 1 1 1 + 4 x 2 + 4 y 2 1 + 4 x 2 + 4 y 2 dA The area of a surface in parametric form Example Find an expression for the area of the surface in space given by the paraboloid z x2 + y2 between the planes z 0 and z 4.To compute the flux through the paraboloid, note that on the paraboloid To compute the flux through R, note that there are two boundaries, the paraboloid, and the unit disk in the plane z = 1. integral in polar coordinates 157 double integral in rectangular coordinates 150 ellipsoid 46 elliptic cone 46 elliptic cylinder 45 elliptic paraboloid. ∫ − 1 1 ∫ − 1 − x 2 1 − x 2 ∫ x 2 + y 2 1 y 3 + z + x 2 &DifferentialD z &DifferentialD y &DifferentialD x = 5 12 &pi F = ∂ x x y 3 + ∂ y y z + ∂ z x 2 z = y 3 + z + x 2.Don't worry, you'll see what I mean in the next article.Apply the Divergence theorem to the vector field F = x y 3 i + y z j + x 2 ⁢ z k and R, the region bounded by the paraboloid z = x 2 + y 2 and the plane z = 1.